15 min read
In this article, we’ll highlight what systematic random sampling is and how you can use it to create random sampling surveys to get a clear understanding of a target population.
If you want a highly effective (and accurate) method for selecting a random sample from a research population, systematic random sampling might be just what you’re looking for. In this article, we’ll break down what systematic random sampling is and how you can use it to get a clear understanding of a target population. Start your free 30-day trial of XM for Strategy & Research today

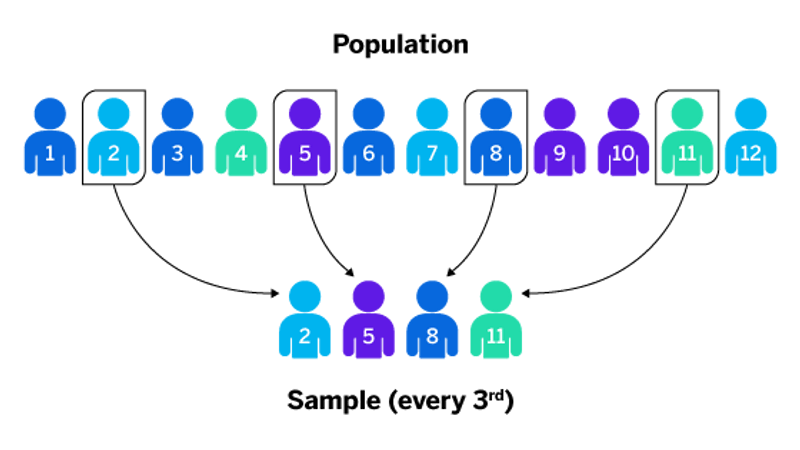
Systematic random sampling is a probability sampling method. This means it uses chance and randomization to select sample data that represents a population. After determining the right sample size, researchers assign a regular interval number they will use to select which members of the target population will be included in the sample. The sample interval (k) is decided by dividing the population size (N) by the sample size (n). If you had a list of 1,000 customers (your target population) and you wanted to survey 200 of them, your interval would be 5. This means that you would sample every 5th person in your list of 1,000 customers. 1,000 / 200 = 5 To ensure a random sample, researchers use a random starting point within the range from 0-k. So if k = 5 you might randomly start with the 2nd name in the list and then sample every 5th person (e.g. 2, 7, 12, 17 and so on).
Although systematic sampling is a relatively simple concept, it can be performed in a few different ways.
This is the ‘classic’ form of systematic sampling where items or individuals are selected at a predetermined interval.
With circular systematic sampling, the sampling process continues past the end of the population list, until the whole population has been sampled.
Linear systematic sampling doesn’t repeat, unlike circular systematic sampling. It produces a number using a form of skip logic to select the sample members.
Systematic sampling can be used whenever you want the benefits of randomly sampling the population you’re studying. It can be especially useful in situations where you don’t have details of the entire population before you begin your study. This is because systematic sampling is rule-based, so you can just apply the interval you’ve chosen to the data. Systematic random sampling is valuable when you’re on a tight budget or a short timescale, but it may not be right for your project if there is any risk of data manipulation.
Systematic sampling can remove some of the unpredictability from a sample, meaning that a researcher could potentially manipulate the results by choosing a starting point that favors their preferred outcome. However, this risk is very slight because the only random component of the sample is the selection of the starting point. After that, the process moves in a set pattern until the sample is complete. For example, in a population of 21 and starting at 1, using an interval of 3 would result in the numbers 3, 6, 9, 12, 15, 18, and 21 being used. It’s also important to ensure that your list is not ordered in any way that could introduce bias, e.g. if your list was ordered male, female, male, female, and you picked every other person, you would introduce a great degree of bias.
Because of the way systematic sampling is structured, surveys based on it are easy to create and the data is easy to analyze. This type of sampling is particularly beneficial where the budget is limited as the sample selection process is straightforward.
While systematic sampling retains an element of randomness, it also introduces some control and process into the selection process.
Systematic sampling carries a low-risk factor because there’s a low chance that the data can be contaminated. This is because of the even distribution of members to form samples.
After the initial starting point, researchers have little control over who gets selected for systematic sampling. The selection process is truly random, creating a buffer against favoritism when it comes to data collection.
Although there are significant advantages to systematic sampling, it can carry some risks that you need to be aware of.
Like all probability sampling techniques, systematic sampling requires that every sample member has a known, non-zero likelihood of being selected. If the true population sizes are not known and cannot be determined, you can’t use the formula k = N/n to determine the sample interval or likelihood of being selected. Another challenge is that it can be difficult to achieve the desired sample size if the true population size is not known in advance. If you need a sample of 200 people, you may not know whether to sample every 5th person or every 10th person.
There’s a way to use systematic sampling when the population size is not known in advance — if you are prepared to guess the interval. Imagine you want to conduct an exit poll after an important election. Although you do not know in advance how many people are going to show up at the election site, you can choose to sample every 5th person who leaves the voting location between when it opens and closes. The true population size will then be approximately 5 times the size of your sample.
If the population you’re assessing has a standard pattern (e.g., the list is ordered male, female, male, female), it can remove the randomness of the sampling interval and inadvertently lead to an unrepresentative sample such as all males. This isn’t common, but it’s worth being aware of before you plan your research project. Let’s say you were surveying a high school class and wanted to select half of the students for an assessment. If the student list was in a boy, girl, boy, girl pattern and your sampling interval was an even number, you could end up with all boys or all girls in your sample. To avoid this, make sure your data is sorted in such a way that won’t introduce any kind of repeating pattern — for example, you could ask the children to line up in order of height. That removes any repeating pattern (e.g., boy, girl, boy, girl) that might interfere with the systematic sample. If you had an electronic list of students in the class, you could sort the list in a random way such as alphabetically by student’s first name.
While systematic sampling is reliable and offers a natural degree of unpredictability and randomness, it’s also open to manipulation by individual researchers, albeit in a limited way. The method the researcher chooses for their sample collection could potentially result in a higher chance of achieving a predetermined outcome, rather than using simple random selection.
It’s easier to achieve the desired sample size when you know the total population of the sample in advance. Once you have this number, the rest of the sampling process is simple.
When you know the size of the sample you want to draw from the population, you can establish the interval needed to achieve the desired sample size from the population.
There are several factors to consider, including population size, the margin of error (confidence interval), and budget.
For example, you may want a sample size that yields a margin of error of +/- 5 points, or maybe it’s determined by your budget, e.g. you’re giving out $10 gift cards but can only afford 200.
For this, you simply divide the total population by the sample size. If the total population size is not known in advance (for example, if you’re conducting an exit poll during an election), then estimate the population size based on historical data (e.g. the previous election) to determine your sampling interval.
Starting your selection at a random number helps to retain the randomness of your selection and removes the risk of cluster or manipulation. The random start number will be between 1 and the sample interval.
E.g. to get a sample of 100 out of 1,000, you would select every 10th person.

Continue choosing your sample members at regular intervals until you have the sample size you need to complete your study.
Let’s say a sample size of 20 out of a population of 100 is required. For this study, each member of the population is assigned a number from 001 to 100.
We first calculate the interval by dividing the total number of people in the population (100) by the number we want in the sample (20). This gives us a sample interval of 5.
We then select a number between 1 and the sampling interval from a random number generator. Let’s say we get 4 — this is where we start. We count down the list (using linear systematic sampling or circular systematic sampling) from our starting point (person 4) and select each 5th person.
For example, if we start at 4, the next would be 9, 14, 19, 24, 29, and so on. When you reach the end of the list, you should have your desired number (20) for the sample size.
A simple random sample is one where every member of the population of interest has an equal probability of being selected, and the selection is done in a completely arbitrary way. You can select randomly from a population using a tool such as a number table or a computer, or by using a draw or lottery system.
Stratified random sampling involves dividing your population into groups (called strata) that are linked by a particular characteristic, such as income bracket or nationality. A random sample is taken from each group, and then these are pooled together to create a random sample of the entire population. The purpose is to make sure each group is represented in your sample.
With cluster sampling, groups rather than individual units of the target population are selected at random for the test. These might be pre-existing groups, such as people in certain zip codes or students belonging to an academic year. Cluster sampling can be done by selecting the entire cluster, or in the case of two-stage cluster sampling, by randomly selecting the cluster itself, then selecting at random again within the cluster.
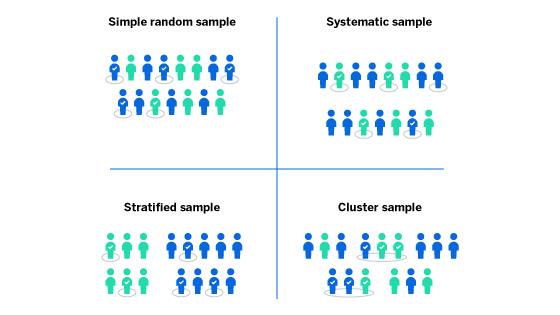
What’s the difference between a systematic sample and a simple random sample?
In each sampling method, every person has an equal chance of being chosen. It’s also true that both methods could create some bias — e.g. a larger percentage of females in the sample than in the population.
The primary reasons to use a systematic sample in place of a random one are
(1) when the population size is unknown in advance (e.g. an exit poll during an election)
(2) if you don’t have an electronic list or you need to sample on the go. For example, you can use systematic sampling to select 1 out of every 5 people that enter a waiting room at a hospital, whereas with a random sample you would need the complete list of patients for the day, which could present problems if things change or last-minute emergencies turn up.
Choosing the right method for sampling your target audience can make all the difference when it comes to the reliability of your data and analysis.
In our guide to sampling methods and best practices, we explore other probability and non-probability sampling methods, including stratified sampling and cluster sampling, convenience sampling, quota sampling, and more — to give you the information you need to conduct comprehensive research.
If you want to learn more about sampling methods, you can read our ultimate guide to sampling methods and best practices.
We specialize in providing solutions that empower everyone to gather research insights and take action. With Qualtrics CoreXM, you can make sophisticated research simple.
Whether you’re in marketing, product development, or HR — with CoreXM, you can rapidly turn insights from surveys into actionable strategies.
Featuring advanced and incredibly flexible survey tools, built-in intelligence (driven by iQ™), a fully automated platform, and research services, CoreXM enables you to run the surveys you need to get answers to your most important marketing, branding, customer, and product questions.
Start your free 30-day trial of XM for Strategy & Research today